Função do 1° Grau
Uma função do 1° grau ou função afim é do tipo f(x) = ax + b, com a e b , sendo que a é o coeficiente de x e b 
, o termo constante.
, o termo constante.
O zero ou a raiz da equação é o valor de x para o qual temos f(x) = 0. Então, se f(x) = ax + b e queremos encontrar f(x) = 0, faremos:
f(x) = 0
ax + b = 0
ax = – b
x = – b
a
ax + b = 0
ax = – b
x = – b
a
Podemos dizer que a raiz de uma equação do 1° grau é dada por x = – b/a.
Função do 2° Grau
Uma função do tipo f(x) = ax² + bx + c, com a, b e c , é uma função do 2° grau ou função quadrática. Os termos a, b e c são ditos coeficientes, e a deve ser necessariamente diferente de zero (a ≠ 0) para que se tenha uma função do 2º grau.
, é uma função do 2° grau ou função quadrática. Os termos a, b e c são ditos coeficientes, e a deve ser necessariamente diferente de zero (a ≠ 0) para que se tenha uma função do 2º grau.
Ela pode ter até duas raízes ou zeros da equação. Para determinar quais são os valores de x, tais que f(x) = 0, nós utilizamos a fórmula de Bhaskara:
O gráfico de uma função do 2° grau é uma parábola. A partir de algumas fórmulas simples, podemos identificar os pontos notáveis da parábola. As coordenadas do vértice da parábola podem ser encontradas através de:
xv = – b
2a
2a
yv = – Δ
4a
4a
Agora que relembramos conceitos importantes sobre funções do 1° e do 2° grau, vamos resolver duas questões sobre função no Enem que caíram em provas anteriores.
(ENEM/2012) Nos shopping centers costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por cada período de tempo de uso dos jogos. Dependendo da pontuação da criança no jogo, ela recebe um certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3,00 e que uma bicicleta custa 9 200 tíquetes.
Para uma criança que recebe 20 tíquetes por período de tempo que joga, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é:
a) 153.
b) 460.
c) 1 218.
d) 1 380.
e) 3 066.
Solução: Para que uma criança que recebe 20 tíquetes por período acumule 9 200 tíquetes (que lhe permitemtrocá-los pela bicicleta), ela deverá jogar por 9 200: 20 = 460 períodos. Como o preço de cada período é de R$ 3,00, o valor gasto será 460 . R$ 3,00 = R$ 1 380,00.
(ENEM/2012) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele e de:
a) 12 kg.
b) 16 kg.
c) 24 kg.
d) 36 kg.
e) 75 kg.
Solução: 30 gotas / x kg = 5 gotas / 2 kg
5 x = 30 . 2
5 x = 60
x = 12
Enem 2014 – Questão 160 – Caderno Amarelo
No Brasil há várias operadoras e planos de telefonia celular.
Uma pessoa recebeu 5 propostas (A, B, C, D e E) de planos telefônicos. O valor mensal de cada plano está em função do tempo mensal das chamadas, conforme o gráfico.
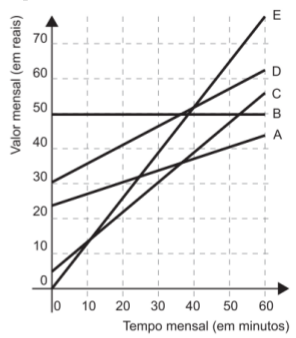
Essa pessoa pretende gastar exatamente R$ 30,00 por mês com telefone.
Dos planos telefônicos apresentados, qual é o mais vantajoso, em tempo de chamada, para o gasto previsto para essa pessoa?
a) A
d) D
b) B
e) E
c) C
d) D
b) B
e) E
c) C
RESOLUÇÃO E COMENTÁRIOS
Alternativa C
A resolução desta questão provém totalmente da interpretação do gráfico. Nele, devemos observar a faixa onde o gasto mensal é R$ 30,00. Em outras palavras, observar a linha horizontal onde o valor no eixo y é 30. Daí, analisando esta faixa, devemos procurar qual das cinco retas cruza a linha horizontal mais à direita. Ela representará o maior tempo mensal de chamadas, em minutos, para o gasto previsto de R$ 30,00, ou seja, a proposta mais vantajosa.
Vamos ao gráfico:
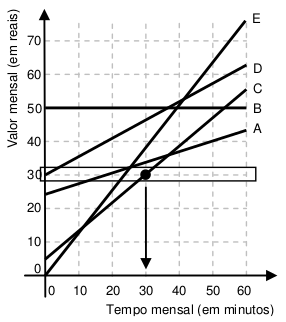
Analisando cada reta, vemos que das cinco, a única que não está na faixa dos R$ 30,00 é a reta B. A reta A, para um gasto de R$ 30,00 permite 20 minutos. A reta C, 30 minutos. Já a reta D não permite nenhum minuto e a reta E um pouco mais de 20 minutos, mas menos que 30.
Logo, dos planos apresentados, o mais vantajoso em tempo de chamadas para um gasto de R$ 30,00 é o plano C.
Comentário: O único conceito necessário para resolver a questão diz respeito à localização de pontos no plano cartesiano.
Conteúdos envolvidos: Interpretação de gráficos.
2.(Enem 2ª aplicação 2010) As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18 bilhões de sacolas plásticas. Os supermercados brasileiros se preparam para acabar com as sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o ano de 2007.
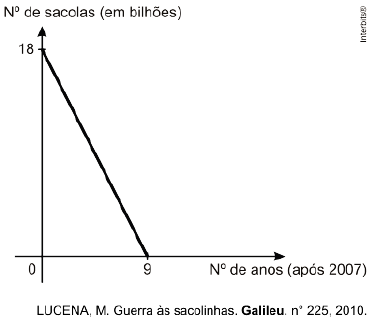
De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidos em 2011?
a) 4,0
b) 6,5
c) 7,0
d) 8,0
e) 10,0
Gabarito: [E]
Seja a função N de R em R, definida por N(n)=na+b em que N(n) é o número de sacolas consumidas, em bilhões, n anos após 2007.
Do gráfico, temos que o valor inicial de 
é 
é
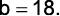
A taxa de variação da função 
é dada por
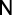é dada por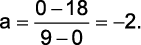
Desse modo, segue que 
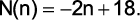
Queremos calcular o número de sacolas consumidas em 2011, ou seja, 
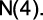
Portanto, 
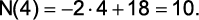
Saiba mais sobre Função Polinomial do 1º grau nesta aula do canal Tenho Prova Amanha, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
3.A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
1ª questão com função – Enem 2013
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei 
, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
Resolução:
Conhecendo a função do 2° grau , seus coeficientes são a = 3/2, b = – 6 e c = C. Vamos então identificar as coordenadas do vértice V da parábola:
, seus coeficientes são a = 3/2, b = – 6 e c = C. Vamos então identificar as coordenadas do vértice V da parábola:
xv = – b
2a
xv = – (– 6)
2.(3/2)
xv = 6
3
xv = 2
yv = – Δ
4a
yv = – (b² – 4.a.c)
4a
yv = – [(– 6)² – 4.(3/2).C]
4.(3/2)
yv = – [36 – 2.3.C]
2.3
yv = – 36 + 6.C
6
yv = – 6 + C
2a
xv = – (– 6)
2.(3/2)
xv = 6
3
xv = 2
yv = – Δ
4a
yv = – (b² – 4.a.c)
4a
yv = – [(– 6)² – 4.(3/2).C]
4.(3/2)
yv = – [36 – 2.3.C]
2.3
yv = – 36 + 6.C
6
yv = – 6 + C
Mas o vértice está localizado no eixo x, logo yv = 0, portanto, temos:
yv = – 6 + C
0 = – 6 + C
C = 6
0 = – 6 + C
C = 6
A altura do líquido é de 6 cm, logo a alternativa correta é a letra e.
4,
